DPC (DPP) Screening Methods for Nonnegative Lasso

Lasso is a widely used spase modeling technique to find sparse representations of an input signal. If we require the coefficients of the sparse representations to be nonnegative, the resulting model is known as the nonnegative Lasso.
Similar to standard Lasso，the DPC screening rule for nonnegative Lasso is also called DPP (Dual Projection onto Polytope).
DPP can be integrated with any existing solvers for nonnegative Lasso. The code will be available soon. The implementation of the DPP rule is very easy.

References

Two-Layer Feature Reduction for Sparse-Group Lasso via Decomposition of Convex Sets. Spotlight
Jie Wang and Jieping Ye.
NIPS 2014. [Code Download]

Formulation of Nonnegative Lasso

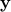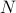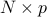Let {bf y} denote the dimensional response vector and ${bf X} = [{bf x}_1, {bf x}_2, ldots, {bf x}_p]$ be the N times p feature matrix. Let 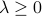lambdageq0 be the regularization parameter. The nonnegative Lasso problem is formulated as the following optimization problem:

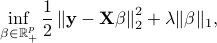
$inf_{beta in mathbb{R}_+^p} frac{1}{2}left|{bf y - X beta}right|_2^2 + lambda |{beta}|_1,$

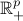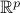where $mathbb{R}_+^p$ is the set of all vectors in $mathbb{R}^p$ with nonnegative components. The dual problem of nonnegative Lasso is

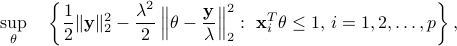
$sup_{theta}quad left{frac{1}{2}|{bf y}|_2^2 - frac{lambda^2}{2}left|theta - frac{{bf y}}{lambda}right|_2^2:,, {bf x}_i^{T}thetaleq 1,,i=1,2,ldots,pright},$

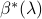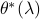We denote the primal and dual optimal solutions of nonnegative Lasso by beta^*(lambda) and theta^*(lambda) , respectively, which depend on the value of 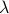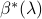lambda . and 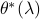are related by

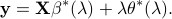
${bf y} = {bf X}beta^*(lambda) + lambda theta^*(lambda).$

Moreover, it is easy to see that the dual optimal solution is the projection of 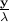$frac{bf y}{lambda}$ onto the dual feasible set, which is a polytope.

Enhanced DPP (EDPP) rule for nonnegative Lasso

Let us define

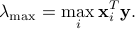
$lambda_{rm max}=max_i{bf x}_i^T {bf y}.$

For all 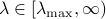$lambda in [lambda_{rm max}, infty)$ , we have

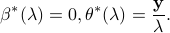
$beta^*(lambda) = 0, theta^*(lambda) = frac{bf y}{lambda}.$

In other words, the nonnegative Lasso problem admits closed form solutions when 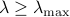$lambda geq lambda_{rm max}$ .

Let $lambda_0 in (0,lambda_{rm max}]$ and lambda in (0,lambda_0] . We define

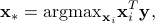
${bf x}_* = {rm argmax}_{{bf x}_i} {bf x}_i^T {bf y},$

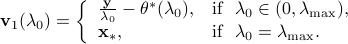
${bf v}_1(lambda_0) = left{ begin{array}{ll} frac{bf y}{lambda_0} - theta^*(lambda_0), & {rm if} hspace{2mm} lambda_0 in (0, lambda_{rm max}), {bf x}_*, & {rm if} hspace{2mm} lambda_0 = lambda_{rm max}. end{array}right.$

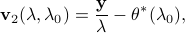
${bf v}_2(lambda, lambda_0) = frac{bf y}{lambda} - theta^*(lambda_0),$

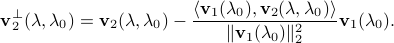
${bf v}_2^{perp}(lambda, lambda_0) = {bf v}_2(lambda, lambda_0) - frac{langle{bf v}_1(lambda_0),{bf v}_2(lambda, lambda_0)rangle}{|{bf v}_1(lambda_0)|_2^2}{bf v}_1(lambda_0).$

EDPP Screening Rule for nonnegative Lasso

For the nonnegative Lasso problem, suppose we are given a sequence of parameter values 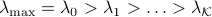$lambda_{rm max} = lambda_0>lambda_1>ldots>lambda_{mathcal{K}}$ . Then for any integer 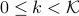, we have $[beta^*(lambda_{k+1})]_i=0$ if 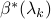is known and the following holds:

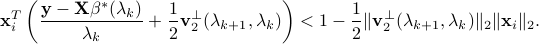
${bf x}_i^Tleft(frac{{bf y}-{bf X}beta^*(lambda_k)}{lambda_k}+frac{1}{2}{bf v}_2^{perp}(lambda_{k+1},lambda_k)right)<1-frac{1}{2}|{bf v}_2^{perp}(lambda_{k+1},lambda_k)|_2|{bf x}_i|_2.$

A Few More Comments of EDPP

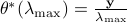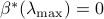To start from $lambda_{rm max}$ , it is worthwhile to note that $theta^*(lambda_{rm max}) = frac{bf y}{lambda_{rm max}}$ and $beta^*(lambda_{rm max}) = 0$ .
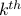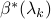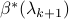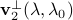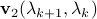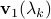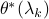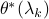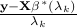At the $k^{th}$ step, suppose that is known. To determine the zero coefficients of $beta^*(lambda_{k+1})$ , EDPP needs to compute ${bf v}_2^{perp}(lambda, lambda_0)$ , which depends on ${bf v}_2(lambda_{k+1}, lambda_k)$ and ${bf v}_1(lambda_k)$ . Thus, we need to compute . Indeed, can be computed by $frac{{bf y}-{bf X} beta^*(lambda_k)}{lambda_k}$ .
After EDPP tells you the zero coefficients of 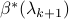$beta^*(lambda_{k+1})$ , the corresponding features can be removed from the optimization and you can apply your favourite solver to solve for the remaining coefficients of 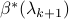$beta^*(lambda_{k+1})$ . Then, go to the next step until the Lasso problems at all given parameter values are solved.