DPC Screening Methods for Standard Lasso

For standard Lasso，the DPC screening rule is called DPP (Dual Projection onto Polytope).
DPP can be integrated with any existing solvers for Lasso. You can either try our code implemented in Matlab to see the performance or integrate it with your favourite solver. The implementation of the DPP rule is very easy.

Publications

Lasso Screening Rules via Dual Polytope Projection. (Improved version of the one accepted by NIPS 2013)
Jie Wang, Peter Wonka, and Jieping Ye.
Journal of Machine Learning Research, to appear.
Lasso Screening Rules via Dual Polytope Projection.
Jie Wang, Jiayu Zhou, and Peter Wonka, Jieping Ye.
NIPS 2013.

Notice that, the Enhanced DPP (EDPP) rule to appear in JMLR is an improved version of the EDPP rule in the NIPS paper. They are NOT the same.

The EDPP rule in the NIPS paper refers to “Improvement 1” in the journal version. The EDPP rule introduced below refers to the one in the journal version.

Formulation of Standard Lasso

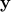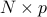Let {bf y} denote the dimensional response vector and ${bf X} = [{bf x}_1, {bf x}_2, ldots, {bf x}_p]$ be the N times p feature matrix. Let lambdageq0 be the regularization parameter. The Lasso problem is formulated as the following optimization problem:

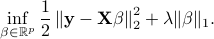
$inf_{beta in mathbb{R}^p} frac{1}{2}left|{bf y - X beta}right|_2^2 + lambda |{beta}|_1.$

The dual problem of Lasso is

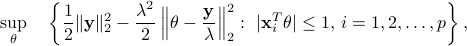
$sup_{theta}quad left{frac{1}{2}|{bf y}|_2^2 - frac{lambda^2}{2}left|theta - frac{{bf y}}{lambda}right|_2^2:,, |{bf x}_i^{T}theta|leq 1,,i=1,2,ldots,pright},$

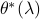We denote the primal and dual optimal solutions of Lasso by beta^*(lambda) and theta^*(lambda) , respectively, which depend on the value of lambda . and 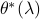are related by

${bf y} = {bf X}beta^*(lambda) + lambda theta^*(lambda).$

Moreover, it is easy to see that the dual optimal solution is the projection of 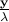$frac{bf y}{lambda}$ onto the dual feasible set, which is a polytope.

Enhanced DPP (EDPP) rule for standard Lasso

Let us define

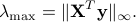
$lambda_{rm max}=|{bf X}^T {bf y}|_{infty}.$

It is well-known that 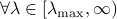$forall lambda in [lambda_{rm max}, infty)$ , we have

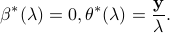
$beta^*(lambda) = 0, theta^*(lambda) = frac{bf y}{lambda}.$

In other words, the Lasso problem admits closed form solutions when 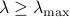$lambda geq lambda_{rm max}$ .

Let $lambda_0 in (0,lambda_{rm max}]$ and lambda in (0,lambda_0] . We define

${bf x}_* = {rm argmax}_{{bf x}_i} |{bf x}_i^T {bf y}|,$

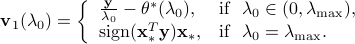
${bf v}_1(lambda_0) = left{ begin{array}{ll} frac{bf y}{lambda_0} - theta^*(lambda_0), & {rm if} hspace{2mm} lambda_0 in (0, lambda_{rm max}), {rm sign}({bf x}_*^T {bf y}){bf x}_*, & {rm if} hspace{2mm} lambda_0 = lambda_{rm max}. end{array}right.$

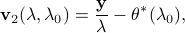
${bf v}_2(lambda, lambda_0) = frac{bf y}{lambda} - theta^*(lambda_0),$

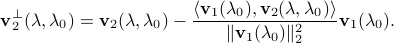
${bf v}_2^{perp}(lambda, lambda_0) = {bf v}_2(lambda, lambda_0) - frac{langle{bf v}_1(lambda_0),{bf v}_2(lambda, lambda_0)rangle}{|{bf v}_1(lambda_0)|_2^2}{bf v}_1(lambda_0).$

EDPP Screening Rule for Lasso

For the Lasso problem, suppose we are given a sequence of parameter values 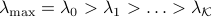$lambda_{rm max} = lambda_0>lambda_1>ldots>lambda_{mathcal{K}}$ . Then for any integer , we have $[beta^*(lambda_{k+1})]_i=0$ if 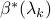is known and the following holds:

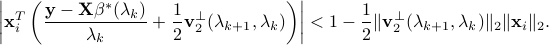
$left|{bf x}_i^Tleft(frac{{bf y}-{bf X}beta^*(lambda_k)}{lambda_k}+frac{1}{2}{bf v}_2^{perp}(lambda_{k+1},lambda_k)right)right|<1-frac{1}{2}|{bf v}_2^{perp}(lambda_{k+1},lambda_k)|_2|{bf x}_i|_2.$

A Few More Comments of EDPP

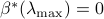To start from $lambda_{rm max}$ , it is worthwhile to note that $theta^*(lambda_{rm max}) = frac{bf y}{lambda_{rm max}}$ and $beta^*(lambda_{rm max}) = 0$ .
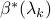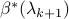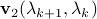At the $k^{th}$ step, suppose that is known. To determine the zero coefficients of $beta^*(lambda_{k+1})$ , EDPP needs to compute ${bf v}_2^{perp}(lambda, lambda_0)$ , which depends on ${bf v}_2(lambda_{k+1}, lambda_k)$ and ${bf v}_1(lambda_k)$ . Thus, we need to compute 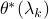. Indeed, 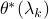can be computed by $frac{{bf y}-{bf X} beta^*(lambda_k)}{lambda_k}$ .
After EDPP tells you the zero coefficients of 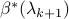$beta^*(lambda_{k+1})$ , the corresponding features can be removed from the optimization and you can apply your favourite solver to solve for the remaining coefficients of 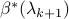$beta^*(lambda_{k+1})$ . Then, go to the next step until the Lasso problems at all given parameter values are solved.